Course code: CSL 201 Course Name: Data Structures Lab
Faculty In Charge: Dr Binu V P
L-T-P-Credits 0-0-3-2
Pre-requisite: CST 201 Data Structures, EST 102 C programming skills.
Operating System to Use in Lab : Linux
Compiler/Software to Use in Lab : gcc
Programming Language to Use in Lab : Ansi C
Preamble: The aim of the Course is to give hands-on experience for Learners on creating and using different Data Structures. Data Structures are used to process data and arrange data in different formats for many applications. The most commonly performed operations on data structures are traversing, searching, inserting, deleting and few special operations like merging and sorting.
/**********************************************************************************/
Lab Cycle-1
Learning Outcome: Learn to use arrays and develop application programs.
(Show the output after completing all the programs. Evaluation is done based on this)
Write C programs to do the following:
1) Write a function rotate(int a[],int n,char d,int cr) to rotate given array elements.
The function will take the array, number of elements in the array, direction of rotation(l-left r-right) and count of rotation( how many times to rotate)
Eg:
input array a[]=2 3 4 5 6 7
rotate(a,6,l,2)
output:4 5 6 7 2 3
rotate(a,6,r,2)
output:6 7 2 3 4 5
2) Find the mean, median and mode of list of elements. Use array to implement the same.(assume Unimode ). Write separate functions.
l=[1,2,3,5,4,5,6,3,1,1]
Mean-3.1
Median-3.0
Mode-1
3) Find the frequency of occurrence of each character in the string ( histogram)
Eg: input: This is a test string
Output:t-3, h-1,i-3,s-4,’ ‘-4…….etc
4)Consider two sets S1={1,2,3,4}, and S2={3,4,5}. Find the intersection of S1 and S2={3,4}.Implement the set operation intersection using arrays.
5)Mark of the students in an exam are stored in an integer array
marks.Sort the marks in descending order using
bubble sort. Implement a function
insert(int m) that inserts the given mark
m into the marks array. The inserted value should maintain a sorted order in the collection.
( understand the complexities involved)
6.Find all local maximums of an array of unique elements. An element is considered to be local max if it is greater than the nearby elements
Eg; [ 3 2 5 7 8 1 6 9]
Here 8 and 9 are local maximums
/**********************************************************************************/
Lab Cycle-2
Learning Outcome: Learn Different Searching and Sorting Techniques.Do the Time and Space complexity analysis of the various algorithms and compare them.
1. Implement Linear SearchSearch an array or list by checking items one at a time.
Time complexity ……………O(n)
2. Implement Binary SearchSearch a sorted array by repeatedly
dividing the search interval in half. Begin with an interval covering the whole array. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. Otherwise narrow it to the upper half. Repeatedly check until the value is found or the interval is empty.Time complexity ……………O(logn)
3. Implement Selection Sort
Find the smallest element in the list and place it in the first position. Repeatedly looks through remaining items to find the least one and moves it to its final location.
Time complexity: O(n^2)
4. Implement Insertion Sort
Sort by repeatedly taking the next item and inserting it into the final data set in its proper order with respect to items already inserted (sorted).
Time complexity: O(n^2)
5. Implement Quick sort
It is also called partition exchange sort. Partition the list recursively and sort the sub lists to obtain the final sorted list.
The time complexity is O(n.log(n))
5. Merge two sorted Arrays.
Given two sorted arrays A:n and B:m. the program should create a sorted array C:m+n by merging them.
6.Implement Merge sort
It is a divide and conquers algorithm. Divide the list recursively and merge the sorted list in each step to obtain the final sorted list.
The time complexity is O(n.log(n))
7. Implement Heap sort
The heap sort works as its name suggests - it begins by building a heap out of the data set, and then removing the largest item and placing it at the end of the sorted array. After removing the largest item, it reconstructs the heap and removes the largest remaining item and places it in the next open position from the end of the sorted array. This is repeated until all elements are sorted.
The time complexity is (n log(n))
/**********************************************************************************/
Lab Cycle-3
Learning Outcome: Learn to do application programs using Searching and Sorting Techniques.
1.Find the K'th smallest element in the array.
solve this problem efficiently using a sorting algorithm The goal is to find the K'th smallest element without fully sorting the entire array.
2. Find the duplicate element from a list.
Hint: Sort the list and count the occurrence of each element.
3. Find the mean, median, mode, and range of the list of values ( This problem is done in cycle-1)
Example 8, 9, 10, 10, 10, 11, 11, 11, 12, 13
The mean is the usual average
(8 + 9 + 10 + 10 + 10 + 11 + 11 + 11 + 12 + 13) ÷ 10 = 105 ÷ 10 = 10.5
The median is the middle value. In a list of ten values, that will be the (10 + 1) ÷ 2 = 5.5th value; that is, I'll need to average the fifth and sixth numbers to find the median:
(10 + 11) ÷ 2 = 21 ÷ 2 = 10.5
The mode is the number repeated most often. This list has two values that are repeated three times.10 and 11
The largest value is 13 and the smallest is 8, so the range is 13 – 8 = 5.
mean: 10.5
median: 10.5
modes: 10 and 11
range: 5
4.Students grade book system keeps rollno, name,mark(out of 100) of 'n' students in an array of structures( Hint : Create an structure student with above mentioned fields).
Read the details of 'n' students and perform the following
a)read a rollno and display the student details
b)display the list in the order of name
c)print a rank list in the descending order of mark
d)display the list of passed students ( marks >=50)
5.Solve the Dutch National Flag Problem:
Problem: Given an array containing only 0s, 1s, and 2s, sort the array in O(n) time.
Challenge: solve this problem with a single pass through the array, without using standard sorting algorithms.
6.Given a list of non-negative integers, arrange them to form the largest number.
/**********************************************************************************/
Lab Cycle-4
Learning Outcome: Learn to use two dimensional arrays.
1.Read a matrix A and a vector v. Write a function which will compute A.v
2.Read a matrix A. Write functions rowsum and colsum which will print the sum of elements in all rows and columns respectively.
3.Consider a
sparse matrix(A sparse matrix is a matrix in which most of the elements are zero).Print the index of all non zero elements and also count them.
4.Saddle Point in a Matrix: Find and print all saddle points (elements that are both the smallest in their row and the largest in their column) in a given matrix.
5.Consider
adjacency matrix of an undirected graph(with out self loops) which is always symmetric and diagonal elements are zero.Input an adjacency matrix and check these properties.Also find the number of edges and degree of all vertices.( Note: The degree of a vertex is the number of edges that are attached to it. The degree sum formula says that if you add up the degree of all the vertices in a (finite) graph, the result is twice the number of the edges in the graph)
6.10.Given an N x N matrix, rotate the matrix 90 degrees clockwise in place
/**********************************************************************************/
Lab Cycle-5Learning Outcome: Learn polynomial representation, sparse matrix representation using arrays and develop application programs.
1. Write a program to read two polynomials and store them in an array. Calculate the sum of the two polynomials and display the first polynomial, second polynomial and the resultant polynomial.
2.Read and polynomial of degree n and store in an array. Evaluate this polynomial for a given value of x.
Eg: 3x^2+2x+1
x=2
evaluation=12+4+1=17
3.Given a sparse matrix . Represent and store it using an efficient method. Also find the sparsity (The sparsity of a matrix can be quantified with a score, which is the number of zero values in the matrix divided by the total number of elements in the matrix.)
4.Input the representation of two sparse matrices. Obtain the representation of their sum.
5.Input the representation of a sparse matrix. Find the representation of its transpose.
6.Check whether the given matrix is sparse symmetric using the representation given.
/**********************************************************************************/
Lab Cycle-6
Learning Outcome: Learn the data structure singly linked list. Linked lists were developed in 1955-56 by Allen Newell, Cliff Shaw and Herbert Simon at RAND Corporation as the primary data structure for their Information Processing Language. IPL was used by the authors to develop several early artificial intelligence programs, including the Logic Theory Machine, the General Problem Solver, and a computer chess program
a linked list is one of the fundamental data structures, and can be used to implement other data structures and has got several applications. It consists of a sequence of nodes, each containing arbitrary data fields and one or two references ("links") pointing to the next and/or previous nodes. The principal benefit of a linked list over a conventional array is that the order of the linked items may be different from the order that the data items are stored in memory or on disk, allowing the list of items to be traversed in a different order. A linked list is a self-referential data type because it contains a pointer or link to another datum of the same type. Linked lists permit insertion and removal of nodes at any point in the list in constant time but do not allow random access. Several different types of linked list exist: singly-linked lists, doubly-linked lists, and circularly-linked lists.
Singly-linked list The simplest kind of linked list is a singly-linked list which has one link per node. This link points to the next node in the list, or to a null value or empty list if it is the final node.
A singly-linked list containing two parts: the data values of the current node and a link to the next node. A singly linked list travels one way.
Write
programs to implement the following using singly linked list:1) Create a linked list with n elements by adding elements at the end.
2) Given a node data, insert a new node after it.
3) Given a node data, insert a new node before it.
4) Insert a new node in the given position.
5) Delete a node, given the key data value.
6) Delete a node given the position.
7) Delete the smallest element from the list.
8) Reverse a list.
9) Search for a given element and print it's position.
10) Create a list in sorted order.
13.Represent a sparse vector using singly linked list. Where each node store the index of non zero element and the element itself.
14.rollno,name and mark of n students are stored using a linked list.Write programs to do insertion,deletion,modification and search operations(use rollno as key).
/**********************************************************************************/
Lab Cycle-7
Learning Outcome: Learn the data structure stack and its applications
Stack
Stack is a data structure having LIFO structure. PC uses stacks at the architecture level, which are used in the basic design of an operating system for interrupt handling and operating system function calls. Recursive programs uses stack extensively. The design of compilers, language recognizers, expression evaluation etc uses stack. Many languages has a class called "Stack", which can be used by the programmer.
2) Implement multiple stacks(2 stacks) using an array. Consider memory efficient implementation
3)Find the minimum element in a stack in O(1) time using an auxiliary stack which keeps track of the minimum element.
4) Implement a sorted push so that stack is always maintained in sorted order.
Using the stack do the following programs
5) Convert a given decimal number into binary and hex.
6) Check whether a string is palindrome.
Expression evaluation and syntax parsing
Calculators employing reverse Polish notation use a stack data structure to hold values. Expressions can be represented in prefix, postfix or infix notations. Conversion from one form of the expression to another form needs a stack. Many compilers use a stack for parsing the syntax of expressions, program blocks etc. before translating into low level code. Most of the programming languages are context-free languages allowing them to be parsed with stack based machines.
7) Check whether the parenthesis are balanced in an expression.
8) Convert a given infix expression to postfix/prefix
9) Evaluate a postfix/prefix expression.
/**********************************************************************************/
Lab Cycle-8Learning Outcome: Learn the data structure Queues.
1. Queue - Implement queue using array and Linked ListQueue a First-In-First-Out (FIFO) data structure. In a FIFO data structure, the first element added to the queue will be the first one to be removed. This is equivalent to the requirement that whenever an element is added, all elements that were added before have to be removed before the new element can be invoked. A queue is an example of a linear data structure.
Queues provide services in computer science and operations research where various entities such as data, objects, or events are stored and held to be processed later. In these contexts, the queue performs the function of a buffer.
2.Circlular Queue ( Ring Buffer)- Implement Using Array A circular buffer or ring buffer is a data structure that uses a single, fixed-size buffer as if it were connected end-to-end. This structure lends itself easily to buffering data streams.
A key advantage of a circular buffer is that it has a static size and elements need not be shuffled around when a portion of the buffer is used. This means that only new data is written to the buffer and the computational cost is independent of the length of the buffer.
It has got number of applications in Computers and communication like implementing a transmission flow control protocol.
3.Priority Queue -Implement Using Array and Linked List One can imagine a priority queue as a modified queue, but when one would get the next element off the queue, the highest-priority one is retrieved first.
There are a variety of simple, usually-inefficient ways to implement a priority queue. They provide an analogy to help one understand what a priority queue is:
Sorted list implementation: Like a checkout line at the supermarket, but where important people get to "cut" in front of less important people. (
O(n) insertion time,
O(1) get-next time)
Unsorted list implementation: Keep a list of elements as the queue. To add an element, append it to the end. To get the next element, search through all elements for the one with the highest priority. (O(1) insertion time, O(n) get-next due to search)
In practice, priority queues blend these two approaches, so any operation takes roughly
O(log(n)) time or less. To get better performance, priority queues typically use a
heap
It has got applications in CPU scheduling and memory management schemes. In a multi user environment the highest priority process must be allocated to the processor.
4.Double Ended Queue –Implement using linked list A deque (short for double-ended queue—usually pronounced deck) is an abstract list type data structure, also called a head-tail linked list, for which elements can be added to or removed from the front (head) or back (tail).
This differs from the queue abstract data type or First-In-First-Out List (
FIFO), where elements can only be added to one end and removed from the other. This general data class has some possible sub-types:
An input-restricted deque is one where deletion can be made from both ends, but input can only be made at one end.
An output-restricted deque is one where input can be made at both ends, but output can be made from one end only.
Both the basic and most common list types in computing, the queues and stacks can be considered specializations of deques, and can be implemented using deques.
5.Reverse a queue using stack( Implement using linked list)
/**********************************************************************************/
Lab Cycle-9Learning Outcome: Learn the data structure doubly linked list and application Doubly-linked list A more sophisticated kind of linked list is a doubly-linked list or two-way linked list. Each node has two links: one points to the previous node, or points to a null value or empty list if it is the first node; and one points to the next, or points to a null value or empty list if it is the final node.
Write programs to implement the following using
doubly linked list:1.Create a doubly linked list with n elements by adding elements at the end.
2.Insert a new node at the front
3.Given a node data, insert a new node after it.
4.Given a node data, insert a new node before it.
5.Insert a new node in the given position.
6.Delete a node, given the key data value.
7.Delete a node given the position.
8.Delete the smallest element from the list.
/**********************************************************************************/
Lab Cycle-10
Learning Outcome: Learn to solve complex problems with singly linked list
1.Write a C program that accepts a linked list as input, and reverses the order of the elements in the list.
2.Implement a program which take two sorted linked lists as input and merges them into a single sorted linked list.
3.Design a program to remove duplicate elements from an unsorted linked list. The order of elements should be preserved.
4.Two sets A and B are represented using linked lists. Create a new linked list representing A-B
5.You are given two linked lists representing two non-negative numbers. The digits are stored in reverse order, and each of their nodes contains a single digit. Write a program to add the two numbers and return the sum as a linked list.(e.g., 123 is represented as 3->2->1).
6.Sort a singly linked list ( use insertion sort)
7.Implement polynomial addition using linked list *
8.Implement polynomial multiplication using linked list *
/**********************************************************************************/
Lab Cycle-11
Learning Outcome: Learn to create, traverse ,modify binary search tree(BST)
A Binary Search Tree (BST) is an acyclic connected graph with one node designated as root node which has the following properties:
· Each node (item in the tree) has a distinct value.
· Each node has at most two children
· Both the left and right subtrees must also be binary search trees.
· The left
subtree of a node contains only values less than the node's value.
· The right subtree of a node contains only values greater than the node's value.
Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets,
multisets, and associative arrays.
The major advantage of binary search trees over other data structures is that the related Search and sorting algorithms can be implemented very efficiently.
Operations Searching Searching a binary tree for a specific value can be a recursive or iterative process. This explanation covers a recursive method.
We begin by examining the root node. If the tree is null, the value we are searching for does not exist in the tree. Otherwise, if the value equals the root, the search is successful. If the value is less than the root, search the left subtree. Similarly, if it is greater than the root, search the right subtree. This process is repeated until the value is found or the indicated subtree is null. If the searched value is not found before a null subtree is reached, then the item must not be present in the tree.
This operation requires O(log n) time in the average case, but needs O(n) time in the worst-case, when the unbalanced tree resembles a linked list (degenerate tree).
Insertion Insertion begins as a search would begin; if the root is not equal to the value, we search the left or right subtrees as before. Eventually, we will reach an external node and add the value as its right or left child, depending on the node's value. In other words, we examine the root and recursively insert the new node to the left subtree if the new value is less than the root, or the right subtree if the new value is greater than or equal to the root.
This operation requires time proportional to the height of the tree in the worst case, which is O(log n) time in the average case over all trees, but Ω(n) time in the worst case.
Deletion There are three cases to be considered:
· Deleting a leaf: Deleting a node with no children is easy, as we can simply remove it from the tree.
· Deleting a node with one child: Delete it and replace it with its child.
· Deleting a node with two children: Suppose the node to be deleted is called N. We replace the value of N with either its in-order successor (the left-most child of the right subtree) or the in-order predecessor (the right-most child of the left subtree).
Tree Traversal Tree-traversal refers to the process of visiting (examining and/or updating) each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.
Compared to linear data structures like linked lists and one dimensional arrays, which have only one logical means of traversal, tree structures can be traversed in many different ways. Starting at the root of a binary tree, there are three main steps that can be performed and the order in which they are performed define the traversal type. These steps (in no particular order) are: performing an action on the current node (referred to as "visiting" the node), traversing to the left child node, and traversing to the right child node. Thus the process is most easily described through recursion.
Preorder
To traverse a non-empty binary tree in preorder, perform the following operations recursively at each node, starting with the root node:
1. Visit the root.
2. Traverse the left subtree.
3. Traverse the right subtree.
(This is also called Depth-first traversal.)
Preorder traversal is used to create a copy of the tree.
Preorder traversal is also used to get prefix expression of an expression tree.
Inorder To traverse a non-empty binary tree in inorder, perform the following operations recursively at each node:
1. Traverse the left subtree.
2. Visit the root.
3. Traverse the right subtree.
(This is also called Symmetric traversal.)
In-order traversal is used to retrives data of binary search tree in sorted order.
Postorder To traverse a non-empty binary tree in postorder, perform the following operations recursively at each node:
1. Traverse the left subtree.
2. Traverse the right subtree.
3. Visit the root.
Postorder traversal is used to delete the tree.
Postorder traversal is also used to get the postfix expression of an expression tree.
Level Order Finally, trees can also be traversed in level-order, where we visit every node on a level before going to a lower level. This is also called Breadth-first traversal.
Sort A binary search tree can be used to implement a simple but efficient sorting algorithm. Insert all the values we wish to sort into a binary search tree—and then do an inorder traversal
“Build a Binary Search Tree and Implement all the operations and Traversals”
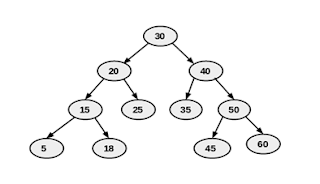
1.Create a binary search tree ( use the sample tree above)(Do the array and linked list implementation)
2.Do the traversals ( do with arrays and linked implementation)
· Inorder -output is {5 , 15 , 18 , 20 , 25 , 30 , 35 , 40 , 45 , 50 , 60}
· Preorder-output is {30 , 20 , 15 , 5 , 18 , 25 , 40 , 35 , 50 , 45 , 60}
· Post Order-output is {5 , 18 , 15 , 25 , 20 , 35 , 45 , 60 , 50 , 40 , 30}
· Level Order-output is {30 , 20 , 40 , 15 , 25 , 35 , 50 , 5 , 18 , 45 , 60}
3.Delete a specified node
4.Search for a given key element ( print found/not found also print the number of comparisons made )
5.Sort a list of elements ( create a BST and do the inorder traversal)
6.Find the maximum and minimum key element
7.Find the height(depth) of a BST
8.Count the number of leaf nodes.
/**********************************************************************************/
Lab Cycle-12
Learning Outcome: Learn to represent Graph and Graph traversals
Represent a graph and Compute the degree of each vertex using the following representations
1. Adjacency Matrix
2.Incident Matrix
3.Adjacency List
4.Implement BFS
5.Implement DFS
/**********************************************************************************/
Lab Cycle-13
learning Outcome: Learn Hash Table and Hash functions
1.Implement a Hash Table with various hash functions.( Division, digit folding, mid square)
2.Implement a Hash Table with chaining.
3.Implement a Hash Table with linear probing.( consider single slot).Compute the load factor.
4.Implement a Hash Table with quadratic probing.( consider single slot).
5.Implement a Hash Table with string as input. Choose suitable hash function.
Comments
Post a Comment